Line And Angle Symmetry
Line And Angle Symmetry
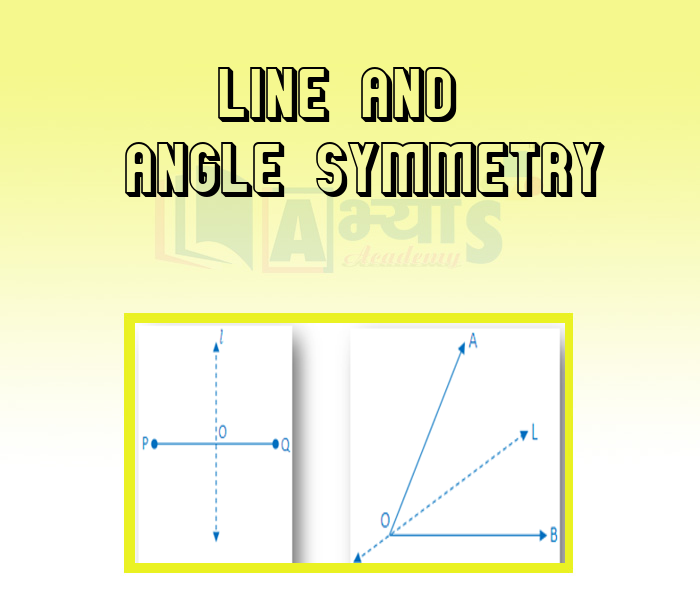
Line :
The geometrical figure line has infinite length as shown in the figure:
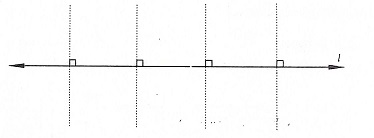
Symmetry of a Line:
Now as we know that a line has infinite length and any line perpendicular to the given line can be considered as a line of symmetry because it will divide the given line into two parts and whenever we fold a line along a line perpendicular to this line one part will overlap the other part. Thus, it can be said that each line perpendicular to the given divide the line into two equal halves(parts). So, a line has infinite number of symmetrical lines which are perpendicular to it. Also, a line is symmetrical to itself.
Line Segment:
A part of line which has a start point and an end point is called a line segment.
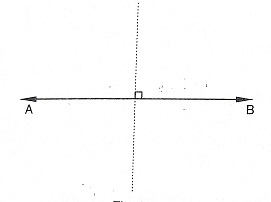
Symmetry of a Line Segment:
As a line segment is of fixed length. so we can draw only one perpendicular line bisector to the given line segment. Thus a line segment has two lines of symmetry, namely, the segment itself and the perpendicular bisector of the segment.
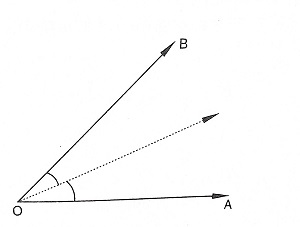
Angle:
Angle is drawn with the help of two intersection lines.
Symmetry of an Angle:
The angle bisector of the angle is a line which divides the angle into two parts such that if we fold an angle along a line which the angle bisector. The two arms defining the angle will overlap each other. Thus an angle with equal arms has one line of symmetry which is along the bisector of the angle.
The line of symmetry for
| |||
| Right Option : B | |||
| View Explanation | |||
A straight angle i.e | |||
| Right Option : D | |||
| View Explanation | |||
. Line of symmetry for an angle is its_____________. | |||
| Right Option : B | |||
| View Explanation | |||
Students / Parents Reviews [20]
Abhyas is a complete education Institute. Here extreme care is taken by teacher with the help of regular exam. Extra classes also conducted by the institute, if the student is weak.
Om Umang
10thWhen I have not joined Abhyas Academy, my skills of solving maths problems were not clear. But, after joining it, my skills have been developed and my concepts of science and SST are very well. I also came to know about other subjects such as vedic maths and reasoning.
Sharandeep Singh
7thAbhyas institute is one of the best coaching institute in the vicinity of Ambala Cantt area. The teachers of the institute are well experienced and very helpful in solving the problems of the students.The good thing of the institute is that it is providing extra classes for the students who are w...
Aman Kumar Shrivastava
10thA marvelous experience with Abhyas. I am glad to share that my ward has achieved more than enough at the Ambala ABHYAS centre. Years have passed on and more and more he has gained. May the centre flourish and develop day by day by the grace of God.
Archit Segal
7thAbhyas Methodology is very good. It is based on according to student and each child manages accordingly to its properly. Methodology has improved the abilities of students to shine them in future.
Manish Kumar
10thMy experience with Abhyas academy is very good. I did not think that my every subject coming here will be so strong. The main thing is that the online tests had made me learn here more things.
Hiya Gupta
8thAbhyas is good institution and a innovative institute also. It is a good platform of beginners.Due to Abhyas,he has got knoweledge about reasoning and confidence.My son has improved his vocabulary because of Abhyas.Teacher have very friendly atmosphere also.
Manish Kumar
10thIn terms of methodology I want to say that institute provides expert guidence and results oriented monitering supplements by requsite study material along with regular tests which help the students to improve their education skills.The techniques of providing education helps the students to asses...
Aman Kumar Shrivastava
10thAbhyas is an institute of high repute. Yogansh has taken admission last year. It creates abilities in child to prepare for competitive exams. Students are motivated by living prizes on basis of performance in Abhyas exams. He is satisfied with institute.
Yogansh Nyasi
7thThird consective year,my ward is in Abhyas with nice experience of admin and transport support.Educational standard of the institute recumbent at satisfactory level. One thing would live to bring in notice that last year study books was distributed after half of the session was over,though study ...
Ayan Ghosh
8thIt has a great methodology. Students here can get analysis to their test quickly.We can learn easily through PPTs and the testing methods are good. We know that where we have to practice
Barkha Arora
10thIt was good as the experience because as we had come here we had been improved in a such envirnment created here.Extra is taught which is beneficial for future.
Eshan Arora
8thThe experience was nice. I studied here for three years and saw a tremendous change in myself. I started liking subjects like English and SST which earlier I ran from. Extra knowledge gave me confidence to overcome competitive exams. One of the best institutes for secondary education.
Aman Kumar Shrivastava
10thAbhyas academy is great place to learn. I have learnt a lot here they have finished my fear of not answering.It has created a habit of self studying in me.The teachers here are very supportive and helpful. Earlier my maths and science was good but now it has been much better than before.
Barkha Arora
10thI have spent a wonderful time in Abhyas academy. It has made my reasoning more apt, English more stronger and Maths an interesting subject for me. It has given me a habbit of self studying
Yatharthi Sharma
10thWe started with lot of hope that Abhyas will help in better understnding of complex topics of highers classes. we are not disappointed with the progress our child has made after attending Abhyas. Though need to mention that we expected a lot more. On a scale of 1-10, we would give may be 7.
Manya
8thMy experience with Abhyas is very good. I have learnt many things here like vedic maths and reasoning also. Teachers here first take our doubts and then there are assignments to verify our weak points.
Shivam Rana
7thAbout Abhyas metholodology the teachers are very nice and hardworking toward students.The Centre Head Mrs Anu Sethi is also a brilliant teacher.Abhyas has taught me how to overcome problems and has always taken my doubts and suppoeted me.
Shreya Shrivastava
8thUsually we see institutes offering objective based learning which usually causes a lag behind in subjective examinations which is the pattern followed by schools. I think it is really a work of planning to make us students grab the advantages of modes of examination, Objective Subjective and Onli...
Anika Saxena
8thMy experience with Abhyas Academy has been very good. When I was not in Abhyas whenever teacher ask questions I could not speak it confidently but when I came in Abhyas, my speaking skills developed and now I am the first one to give the answer of teachers question.
